เว็บไซต์ calcoolacademy.com เป็นเว็บไซต์เรียนแคลคูลัสออนไลน์ที่สมบูรณ์แบบที่สุด

เนื้อหาหัวข้อนี้สอนถึง การหาอนุพันธ์ของฟังก์ชันที่ x กับ y เขียนอยู่ในรูปตัวแปรต้นตัวเดียวกัน เช่น 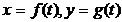 ถ้ายกตัวอย่างสมการคือ สมการของการเคลื่อนที่ โดยที่  x เป็นเคลื่อนที่ในแนวราบและ y เป็นเคลื่อนที่ในแนวดิ่ง ของวัตถุๆหนึ่ง โดยมีเวลา t เป็นเงื่อนไขของการเคลื่อนที่ ซึ่งเราก็สามารเขียนความสัมพันธ์ร่วมกันได้ระหว่าง x กับ y โดยมีตัวแปร t เป็นตัวเชื่อมกัน และเราจะเรียนรู้เพื่อหาอนุพันธ์ สำหรับใช้หาความเร็วและความเร่งในเรื่องการประยุกต์ของอนุพันธ์